Three Tiling Theorems
17 crystallographic groups theorem
Also known as the 17 wallpaper groups theorem. Any periodic tiling of the plane will have a symmetry group isomorphic to one of the seventeen groups listed in the table below. A detailed description of these groups can be found here.
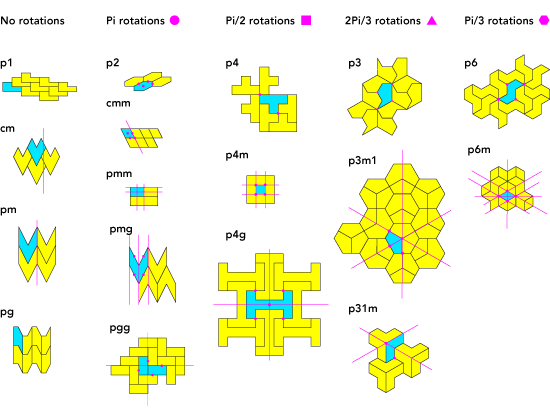
All the possible symmetries of a periodic tiling have to be reflections, glide reflections, or rotations of order 2, 3, 4 or 6.
Undecidability theorem
There is no procedure for deciding whether or not an arbitrary body or set of bodies admits a tiling of the plane.
Extension theorem
If a finite set of bodies can be arranged to tile regions that contain arbitrarily large discs, then the set of bodies will tile the plane. (These regions don't need to be nested, and none of the tilings of the regions need to be extendable).